연구의 첫 단추, 표본수의 계산 G*Power

“가장 중요한 것이 연구 질문에 답하기 위한
적절한 표본수를 결정하는 것이다.”

글 최관우(원광보건대학교)

논문 작성 시 유용한 프로그램

연구 진행에 있어 전체 모집단으로 연구를 수행할 수 있다면 보다 정확한 결과를 얻을 수 있다. 그러나 대부분의 연구는 전체 모집단을 대상으로 연구를 수행하지 않는다. 왜냐하면 모집단을 전수 조사하는 것이 불가능하지 않더라도 시간과 돈, 노력의 낭비로 이어져 비실용적이며 비효율적이기 때문이다. 따라서 대부분의 연구는 전체 모집단을 대표하는 표본을 선택하고, 선택된 표본으로부터 데이터를 획득하며, 획득된 데이터에 통계 기법을 적용하여 모수를 추정한다. 이러한 과정에서 가장 중요한 것이 연구 질문에 답하기 위한 적절한 표본수를 결정하는 것이다.

연구에 있어 표본수는 너무 작아도 안되고 너무 커서도 안된다. 왜냐하면 표본수가 너무 작을 경우 관찰된 유의미한 차이가 무작위적 변이에 의해 발생했을 가능성을 배제할 수 없으며, 반대로 표본수가 너무 클 경우 연구자가 평가하려는 변수보다 너무 많은 변수가 통계적으로 유의미해질 수 있기 때문이다. 따라서 표본수를 적절하게 설정하는 것이 매우 중요한데 이러한 표본수는 연구의 귀무가설과 대립가설, 효과크기, 검정력(1-β), 유의수준(α), 제1종 오류, 제2종 오류, 통계분석 유형에 따라 결정된다. 그러다 보니 일반 프로그램으로 계산하기에는 전문적인 통계 지식과 프로그래밍이 필요해 너무 복잡하고 어려우며, 시판되고 있는 상용 프로그램을 사용하기에는 가격이 비싸 비용이 너무 많이 든다는 문제점이 있다.

G*Power(Heinrich-Heine-Universität Düsseldorf, Düsseldorf, Germany)는 표본 크기 및 검정력(Power)을 무료로 계산해 주는 소프트웨어로 적절한 표본수를 산출할 때 매우 유용한 프로그램이다. 즉, 연구에 들어가기 전 “어느 정도의 표본수가 필요한가?” 라는 질문에 답을 하기 위해 사용할 수 있는 프로그램으로, 보통 IRB 승인을 받거나 연구 논문의 proposal 시 심사자(reviewer) 들에게 표본수 산출의 명확한 근거를 제시하여야 할 때 유용하게 사용된다. G*Power는 현재 3.1.9.7 버전까지 나와있으며 윈도우와 맥 운영체제에서 모두 사용 가능하고 다운로드는 https://www.psychologie.hhu.de/arbeitsgruppen/allgemeine-psychologie-und-arbeitspsychologie/gpower에서 받을 수 있으며 홈페이지에 간단한 사용방법도 제공하고 있다.

G*Power를 이용하면 F-test, t-test, x²-test, z-test, families and some, exact tests와 같은 통계 분석에 대해 통계적 검정력을 분석을 할 수 있다. 분석은 α(유의수준), 1-β(검정력), Effect size, N(Sample size), Df(자유도) 등의 parameter 값을 이용해 분석하는데 실제 연구 진행시 유의수준, 검정력, Effect size 등등을 입력 했을 때, 적절한 표본수를 산출해 준다. 이중 Effect size는 표본수나 검정력을 계산하기 위해서 필수적인 parameter지만 통계 전문가가 아닌 경우에는 계산하기가 어렵다는 특성이 있다. G*Power에서는 이러한 어려움을 덜기 위해서 Effect size를 자동으로 계산해주는 모듈을 탑재하고 있으며, 특히 분포 함수(distribution function)와 분석 디자인(contingency table 등)과 같은 부수적인 인터페이스를 도입해 쉽게 사용 할 수 있게 하였다.

그럼 간단히 G*Power의 사용법에 대해 알아보자. 프로그램을 설치하고 실행시키면 아래와 같은 화면이 나타난다.

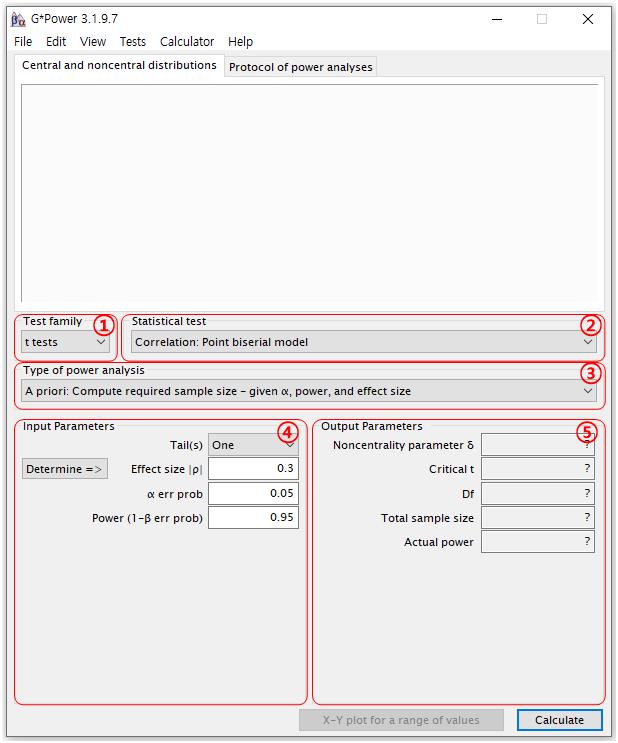
① Test family: 내가 사용할 통계 Test의 큰 범주 선택
-t test 쓸 때는 t test 선택
-Anova, Manova, Ancova, Mancova 쓸 때는 F test 선택

② Statistical test: ①에서 선택한 통계의 세부 항목 선택

③ Type of power analysis: 어떤 분석을 할 지 지정
-표본수를 구할 때 “A priori: Compute required sample size–given α, power, effect size”를 선택

④ Input Parameters: α 값과 Power, Effect size를 지정

⑤ Output Parameters: 결과값을 보여주는 창

사용법은 아주 간단한데, 화면에 표시된 1부터 4까지의 항목을 선택 또는 입력 후 오른쪽 하단의 Calculate 버튼을 누르면 최종결과가 5번 항목에 나타난다. 이를 좀 더 자세히 살펴보면 우선 Test family와 Statistical test에서 통계분석의 종류를 선택한다. 그리고 Type of power analysis에서 통계적 검정력 분석을 어떤 목적으로(필요 표본수 계산, 검정력 계산 등) 수행할 것인지를 선택한다. 마지막으로 Input parameters에서 각 parameter들을 자신의 연구 상황에 맞게 설정해주고, Calculate 버튼을 클릭하면 계산을 자동으로 수행해준다.

예를 들어, 독립표본 t검정(independent sample t-test)으로 두 그룹을 비교할 때, 중간 정도의 효과크기를 가지고, 유의수준 0.05이며 검정력(Power) 0.8 정도를 원할 때(보통 일반적으로 사용되는 수준) 필요한 표본수를 구해보도록 하자.

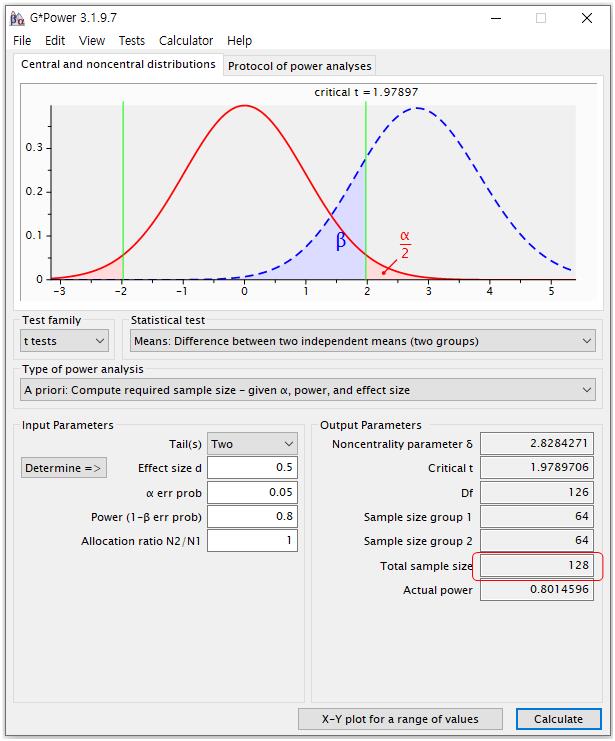
① Test family에는 t tests를 선택

② Statistical test에는 Means: Difference between two independent means (two groups) 선택 → 독립적인 두 그룹에서의 평균 비교분석

③Type of power analysis에는 A priori: Compute required sample size-given α, power, and effect size 선택 → 말 그대로 특정 알파값, 파워, 효과크기에서 필요한 표본수를 구하는 priori(미리 해 보는 분석)

④ Input Parameters에는
-Tail(s): Two → 양측 또는 단측검정을 선택하는 곳으로, 보통 많이 쓰는 양측검정은 Two를 선택
-Effect size d: 0.5 → 효과크기를 설정하는 곳으로(정확히는 t-test에서의 효과크기를 알 수 있는 cohen’s d 값을 말함), small, medium, large 중 보통 medium 정도의 효과크기를 입력하면 됨(t-test에서 medium 정도의 효과크기는 0.5)
-α err prob: 0.05 → 유의수준을 설정
-Power: 0.8 → 보통 0.8로 또는 0.95로도 많이 설정
-Allocation ratio N2/N1: 1 → 두 그룹의 표본수 비를 정하는 것으로, 두 그룹에 동일한 표본수를 넣고 싶으면 1, 한 그룹이 다른 그룹보다 2배 많게 표본수를 넣고 싶으면 2라고 설정(보통은 1)

위와 같이 설정하였을 때 최종 적절한 표본수는 128명으로 산출된다. 이때, 효과 크기를 large로 바꾸거나, 유의수준을 0.01로 낮추거나 혹은 검정력(Power)을 0.95로 높일 경우 연구의 정확도는 높아지지만 표본수가 증가되는데, 이를 결정하는 것은 연구자의 몫으로 위에서 제시한 설정값은 일반적인 정도라고 생각하면 된다.

다른 예로, 일원배치분산분석(one way ANOVA)을 이용하여 세 그룹을 비교할 때 원하는 표본수를 계산하기 위해서는 다음과 같이 설정하면 된다.

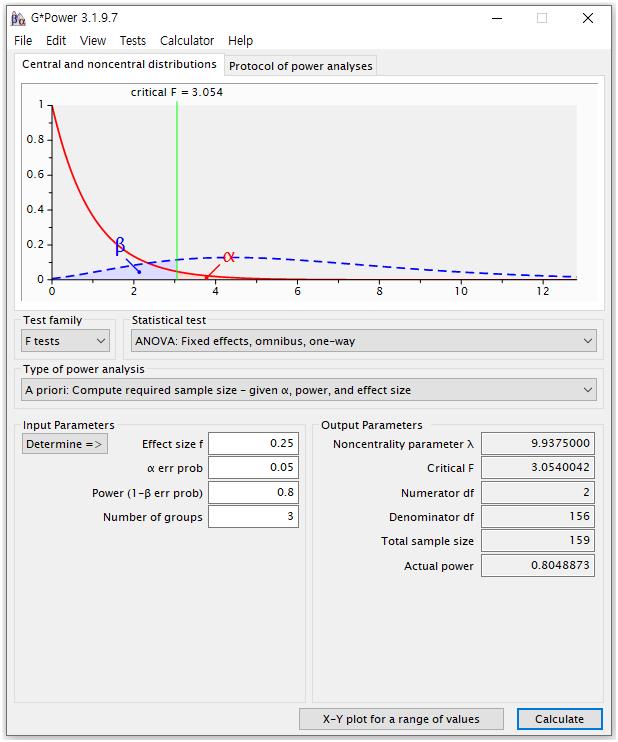
① Test family: F tests

② Statistical test: ANOVA: Fixed effects, omnibus, one-way

③ Type of power analysis: A prior: Compute required sample size-given α, power, and effect size

④ Input Parameters:
-Effect size f: 0.25
-α err prob: 0.05
-Power: 0.8
-Number of groups: 3

그러면 최종 표본수는 159명이 나오는데, 참고로 일원배치(one-way) 이외에 이원배치(2-way) 이상의 ANOVA, ANCOVA 분석을 사용 할 때에는 ②의 Statistical test 중에서 자신이 원하는 분석으로 선택하면 된다.

마지막으로 회귀분석에 필요한 표본수를 계산하기 위해서는

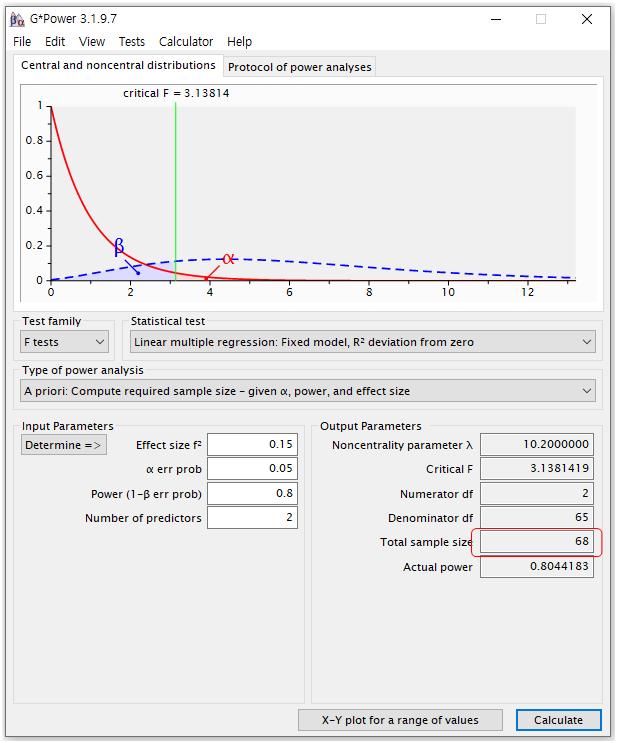
① Test family: F tests

② Statistical test: Linear multiple regression: Fixed model, R2 deviation from zero

③ Type of power analysis: A priori: Compute required sample size-given α, power, and effect size

④ Input Parameters:
-Effect size f²: 0.15
-α err prob: 0.05
-Power: 0.8
-Number of predictors: 2로 설정하면 쉽게 연구에 필요한 적절한 표본수를 산출할 수 있다.

마지막으로 G*Power를 사용하여 표본수를 산출하였다면 산출 근거에 대한 참고문헌은 다음 내용을 삽입하면 된다.

1. Faul, F., Erdfelder, E., Lang, A.-G., & Buchner, A. (2007). G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39, 175-191.
2. Faul, F., Erdfelder, E., Buchner, A., & Lang, A.-G. (2009). Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses. Behavior Research Methods, 41, 1149-1160.